TL;DR

Challenge 26 in Cryptopals.

As if the swiss-army knife of encryption (i.e. the XOR operation) had nothing more to give, we’re presented with yet another sleight of hand that teach us one more lesson:

good random bits are not for free, but are worth the cost.

In CBC mode, we know that we have to come up with two blocks of 16 random octets:

• the key
• the Initialization Vector.

Heck, I even reused the same function in a previous challenge to generate both (although the function generates a different block every time it’s invoked):

sub the_key { state $key = random_key() }
sub the_iv  { state $iv  = random_key() }

Good random data can be tricky to generate (at least, to generate quickly for a certain level of confidence), so it’s tempting to pre-share the key and double it down as the IV, with the added benefit that we will not need to send it.

Like in those contracts with a lot of details in small writings, this is a thing that we MUST NOT do and will void our warranty.

Let’s start from that image from Wikipedia:

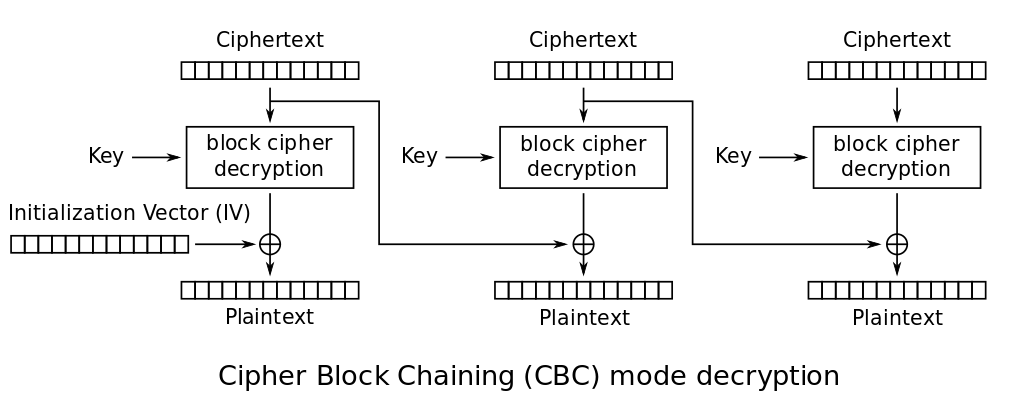
When decrypting the first block of ciphertext $C_1$, the plaintext we get is:

where $K$ is the key (doubling down as IV) and $f’(C_1)$ is the block decryption (via AES in our case) of the first block of ciphertext $C_1$.

The challenge suggests to submit the three blocks $C_1 \mathbf{0..0} C_1$ for decryption, which means that the plaintext we get for the third block is:

The challenge tells us that we will be able to get our hands on both $P’_1 = P_1$ and $P’_3$, thanks to some aggressive logging that is too eager to fix bugs and less careful to leak sensitive data. This leads to the disastrous consequence:

This tells us two things:

• whatever involves security and errors should be as boring as possible. The exact, same, boring answer given back with the best poker face, without any hint of any difference. Just Say No [to Griff].
• quality random data might be expensive, but reusing them makes them very less random and, like in this case, very deterministic.

Putting this into Perl code we obtain the following:

#!/usr/bin/env perl
use v5.24;
use warnings;
use experimental 'signatures';
no warnings 'experimental::signatures';

use File::Basename 'dirname';
use lib dirname(__FILE__);
use CryptoPals ':all';

use Test::More;

# Alice, encrypting three blocks of ASCII-only plaintext
my $alice_plaintext = 'YELLOW SUBMARINE' x 3;
my $alice_ciphertext = encrypt($alice_plaintext);

# This works for Bob on the receiving side
my $bob_dec_1 = oracle_decryption($alice_ciphertext);
is $bob_dec_1->{outcome}, 'OK', 'decryption when ciphertext is fine'
   or diag(''. xxd($bob_dec_1->{data}));

# Now suppose that Eve got in the way instead
my $alice_ciphertext_b1 = substr $alice_ciphertext, 0, 16;
my $eve_ciphertext = join '', $alice_ciphertext_b1, ("\x00" x 16),
   $alice_ciphertext_b1;
my $bob_dec_2 = oracle_decryption($eve_ciphertext);
is $bob_dec_2->{outcome}, 'ERROR', 'decryption when ciphertext is wrong';

# And the leaked "wrong" decrypted data is a gold mine
my $leaked = $bob_dec_2->{data};
my $p_1 = substr $leaked, 0 * 16, 16;
my $p_3 = substr $leaked, 2 * 16, 16;
my $retrieved_key = $p_1 ^ $p_3;
is $retrieved_key, the_key(), 'key retrieval successful';

done_testing();

sub encrypt ($plaintext) {
   aes_cbc_encrypt($plaintext, the_key(), the_iv());
}

sub oracle_decryption ($ciphertext) {
   my $dec;
   my $ok = eval {
      $dec = aes_cbc_decrypt($ciphertext, the_key(), the_iv());
      $dec = validate_pkcs7_pad($dec, 16);
      1;
   };
   return { outcome => ERROR => data => $dec }
      if (! $ok)  || grep { ord($_) > 0x7F } split m{}mxs, $dec;
   return { outcome => 'OK' };
}

sub the_key { state $key = random_key() }
sub the_iv  { the_key() }

I think there’s a slight chance of not getting the key, or all of it, back. This might happen with a very, very low probability. In particular:

• if the padding of the third block happens to be correct, the last byte might be stripped out (although, in this case, it would be easily recoverable and might be re-added to $P’_3$)
• if, in addition, the whole decrypted stuff only contains ASCII characters, we will not get back anything!

OK, not a reasonable corner case to keep in mind in these challenges…

Stay safe and secure!