TL;DR

We start a series of posts on solving the puzzle aquarium, which is nice and relaxing. We will address this as an exercise in constraint programming.

Aquarium is one of many puzzles that can be played freely online, most (all?) of which are good candidates to programmatic solutions using constraint programming. Or, at least, I think so.

Let’s take one

We will work on an example mainly, which is the 6x6 easy puzzle that goes by identifier 681,742. Why this? It was the one that appeared randomly when opening the site. This is a screenshot of the puzzle:

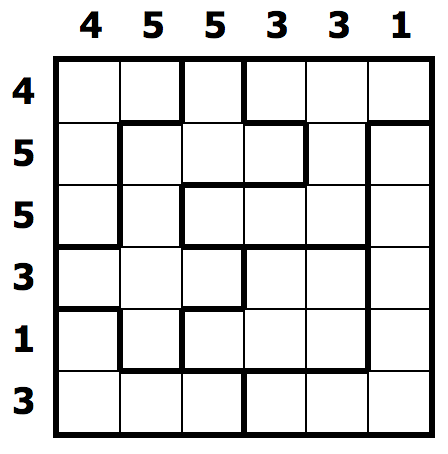
With a bit of cheating (i.e. reading the page source) we can get a synthetic description of the puzzle, in Javascript:

var task = '4_5_5_3_3_1_4_5_5_3_1_3;1,1,2,3,3,3,1,2,2,2,3,4,1,2,3,3,3,4,2,2,2,5,5,4,6,2,5,5,5,4,6,6,6,4,4,4'

It’s not difficult to recognize what those numbers are for:

• underscore-separated values before the semicolon represent the number of water-filled squares by column and by row respectively (half and half)
• all values after the semicolon, separeated by commas, represent the aquarium identifier that a specific square belongs to, starting from the upper-left corner and going right, then down.

The following picture makes the mapping easier to read.

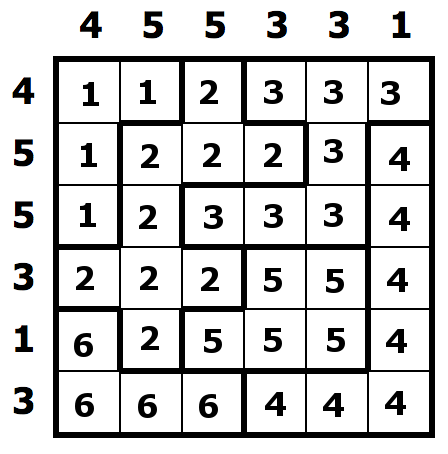
Let’s suppose that we save this whole string into a file:

$ cat example.aqp
4_5_5_3_3_1_4_5_5_3_1_3;1,1,2,3,3,3,1,2,2,2,3,4,1,2,3,3,3,4,2,2,2,5,5,4,6,2,5,5,5,4,6,6,6,4,4,4

Let’s parse it

There Is More Than One Way To Do It, right? A first approach might be the clean one, like follows:

• first of all divide the two halves by the semicolon
• the first half is then split on the underscore, half of it goes into one array and the other half goes in the other
• the second half is split on the comma, then we take elements $N$ by $N$ (where $N$ is the size of one of the arrays in the previous bullet).

We’re not here to make things clean, right? We should… but let’s consider that:

• we have to deduce $N$ anyway…
• three split when we can do one?!?

So, let’s just do one split over sequences of non-digit characters:

# guess what's inside $puzzle_text?
my @items = split m{\D+}mxs, $puzzle_text;

Now we have to find $N$. Aquarium puzzles are always $N \times N$ grids, to which we add $2 \cdot N$ to account for the column and row constraints. Hence, the total number $T$ of items in @items is:

which is a simple quadratic equation whose positive root is:

that translates into:

my $n = sqrt(@items + 1) - 1;

Now, it’s just a matter of splicing the array:

my @items_by_col = splice @items, 0, $n;
my @items_by_row = splice @items, 0, $n;
my @field        = map { [splice @items, 0, $n] } 1 .. $n;

Test time!

Let’s consider a simple program to read the input puzzle and dump what we parse according to the algorithm above:

#!/usr/bin/env perl
use 5.024;
use warnings;
use autodie ':all';
use English '-no_match_vars';
use experimental qw< postderef signatures >;
no warnings qw< experimental::postderef experimental::signatures >;

my $puzzle = load_puzzle(shift);

use JSON::PP;
say encode_json $puzzle;

sub load_puzzle ($filename) {
   my $fh =
     $filename eq '-'    # filename '-' means 'read from standard input'
     ? \*STDIN
     : do { open my $fh, '<', $filename; $fh };

   # just get everything
   my @items        = split m{\D+}mxs, scalar readline $fh;
   my $n            = sqrt(@items + 1) - 1;
   my @items_by_col = splice @items, 0, $n;
   my @items_by_row = splice @items, 0, $n;
   my @field        = map { [splice @items, 0, $n] } 1 .. $n;

   return {
      n            => $n,
      items_by_col => \@items_by_col,
      items_by_row => \@items_by_row,
      field        => \@field,
   };
} ## end sub load_puzzle ($filename)

On our example file (output is adjusted with spaces/indents for clarity):

$ perl aquarium-01.pl example.aqp
{
    "field":[
        ["1","1","2","3","3","3"],
        ["1","2","2","2","3","4"],
        ["1","2","3","3","3","4"],
        ["2","2","2","5","5","4"],
        ["6","2","5","5","5","4"],
        ["6","6","6","4","4","4"]
    ],
    "items_by_row":["4","5","5","3","1","3"],
    "items_by_col":["4","5","5","3","3","1"],
    "n":6
}

Looks good!

A word on the data structure

To summarize, we parsed the input into a hash reference that contains the following keys:

• n is the size of the puzzle. It’s not strictly needed, but it makes things simple and we’ll leave it;
• items_by_col is an array reference that contains the constraints over the columns. In particular, the $i$-th slot in the array contains the number of water-filled squares in the $i$-th column (counting from left to right);
• items_by_row is an array much like items_by_col, but for rows (counting from top to bottom);
• field is an array-of-arrays (AoA), where the outer array (reference) holds references to arrays representing rows from the whole grid. Each single item holds the identifier of the aquarium it is part of.

In addition to the parsed items above, we will also consider a further optional key:

• status holds the (possibly partial) solution of the puzzle. It is an array-of-arrays where the item in the $i$-th row and $j$-th column can be one of:
  • 0: this cell has not been decided yet;
  • 1: this cell is filled with water;
  • -1: this cell is empty.

Interested?

This is hopefully the first of a series of post about a solver for aquarium. All code will be put in repository aquarium-solver for those interested… this first post is related to 01/aquarium.pl.

Until next time, happy coding!