ETOOBUSY 🚀 minimal blogging for the impatient
A 4-faces die from a 6-faces die
TL;DR
How can we simulate a die with 4 faces with a die that has 6?
Some games require rolling a 4-sided die to get some random outcome in a specific phase. This is usually accomplished using… a 4-sided die (also known as D4), usually a regular tetrahedron (which has, indeed, 4 faces).
What can we do if we only have a more commong 6-sided die instead, i.e. a cube or D6 in playing jargon? Let’s take a look.
Warm up: a coin from a D6
Let’s start simple and try to generate the outcome of a fair two-sided coin from a fair D6 die. Our goal is to generate Heads with probability $\frac{1}{2}$ and Tails with probability $\frac{1}{2}$:
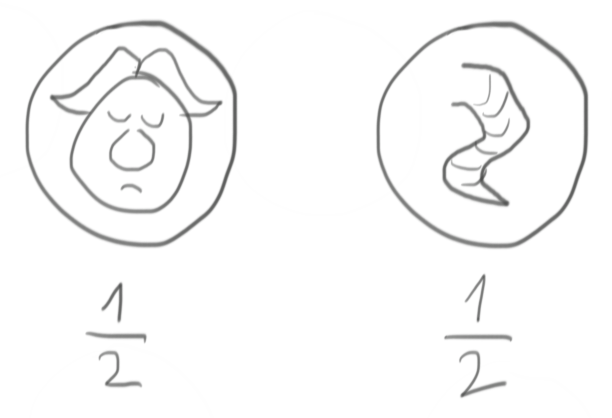
We have a (hopefully fair!) die at our disposal, i.e. a device that is capable of generating each of its faces with probability $\frac{1}{6}$:
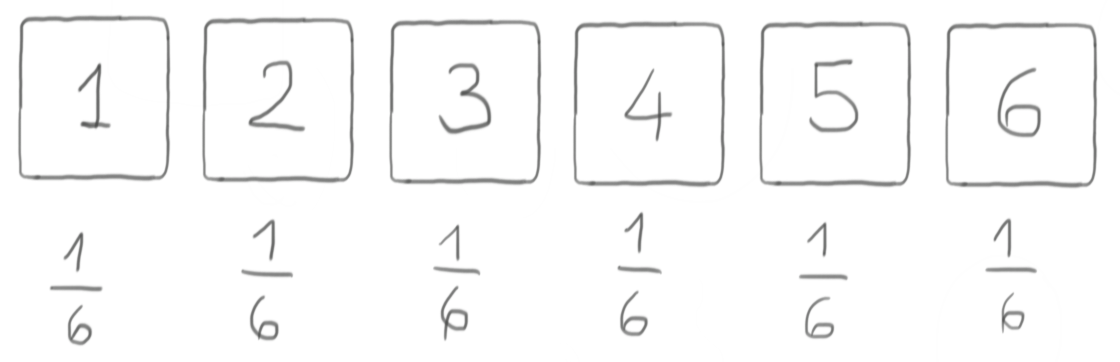
Let’s take any three faces of the die (e.g. 1, 2, and 3) and ask: what is the probability of a single roll to give us one of them? It’s the sum of the respective probabilities, i.e. $\frac{1}{6} +\frac{1}{6} + \frac{1}{6} = \frac{1}{2}$.

We’re definitely onto something, because at this point we can do the following association:
- if the D6 roll gives us either 1, or 2, or 3, then our virtual coin says Heads
- otherwise, our virtual coin says Tails.
and we are sure that our virtual coin is fair (as long as the D6 is fair, or course!).
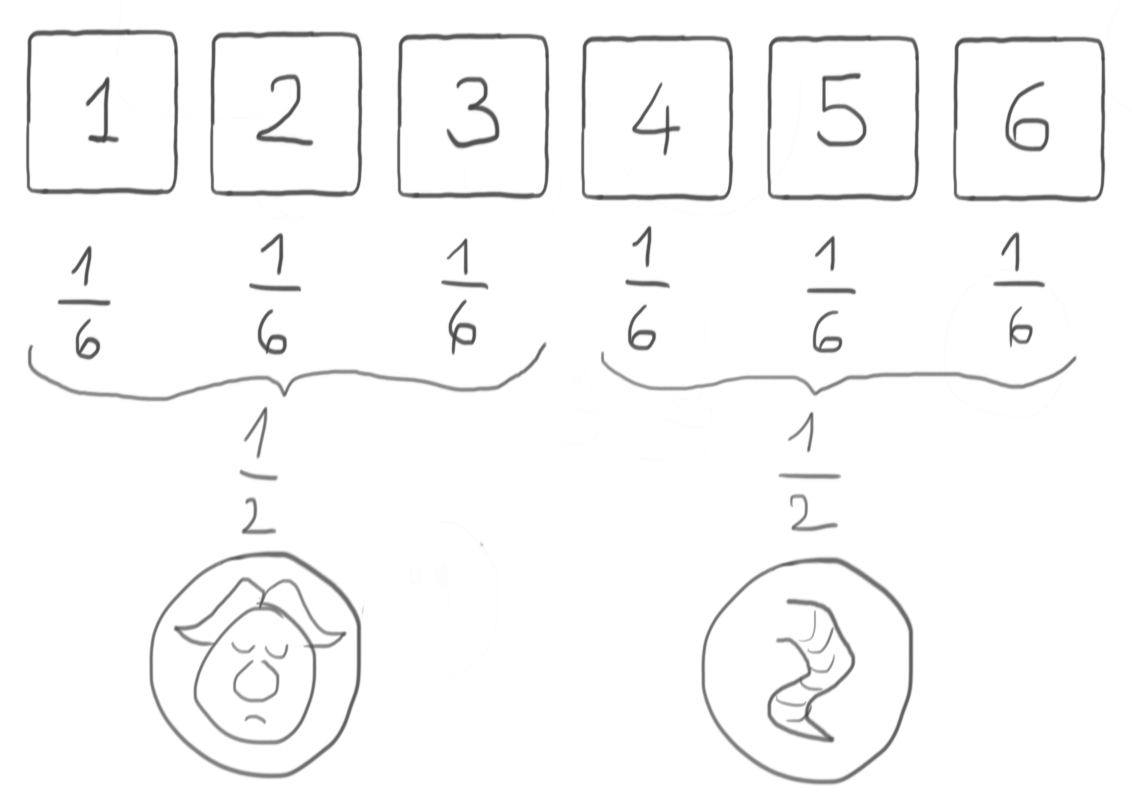
Any three-faces subset of the D6 will do, of course: you might choose e.g. to take odd values for Heads and even values for Tails, or whatever else you like. The important thing is that you decide this before rolling the die!
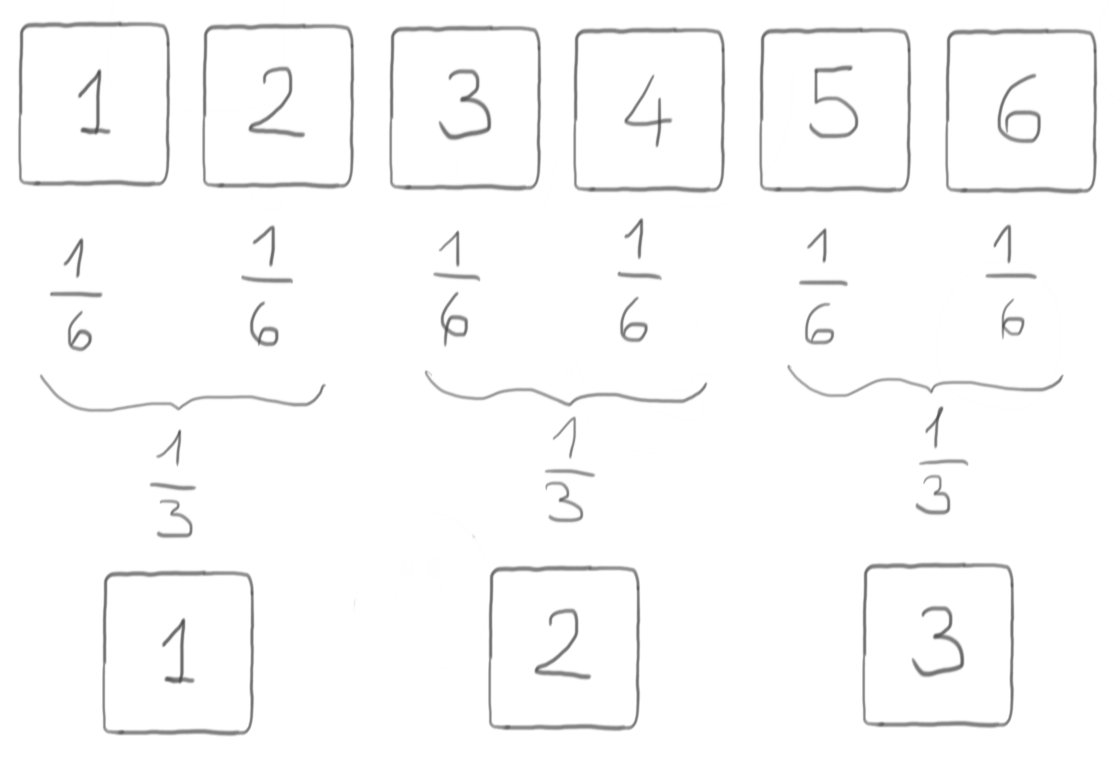
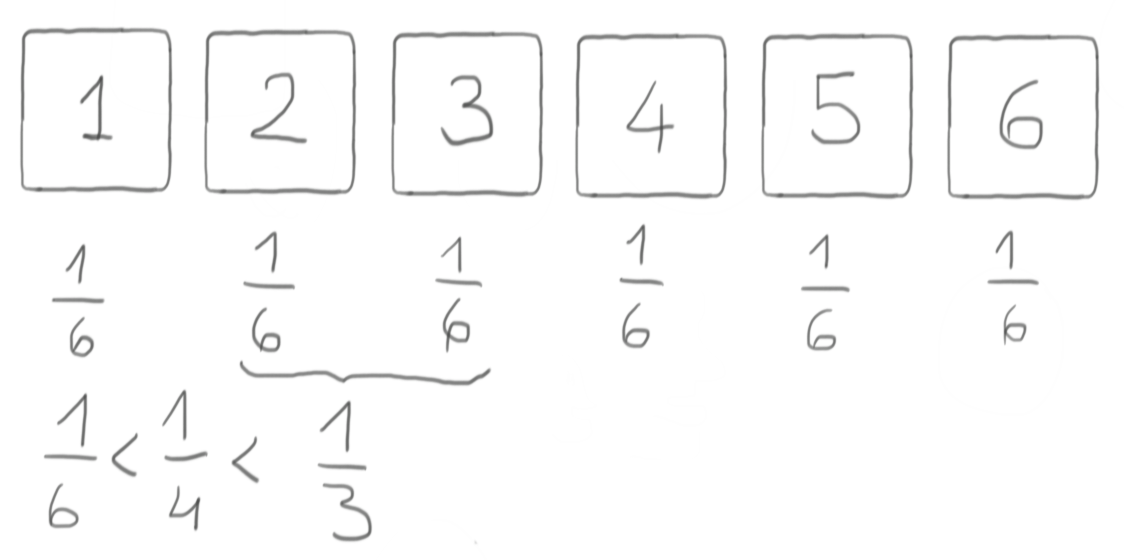
One step ahead: a D3 from a D6
It’s easy to extend the previous section to also enable generating a 3-sided die from a D6: just group the D6 faces in pairs, and each of them will have probability $\frac{1}{3}$ to come out from a single roll, thus giving us a virtual D3. Again, it’s important to decide beforehand what is the virtual D3 value associated to each pair, e.g. like in the following picture.
OK, what about a D4?
The two examples above were easy because it’s easy to combine faces with an outcome probability of $\frac{1}{6}$ into the needed output probabilities (respectively of $\frac{1}{2}$ for the virtual coin and $\frac{1}{3}$ for the virtual D3). At the end of the day, it depends on $6$ being divisible by both $2$ (for the virtual coin) and $3$ (for the virtual D3).
On the other hand, the D4 is a different beast because $6$ is not divisible by $4$, so we cannot recombine $\frac{1}{6}$-sized pieces to obtain $\frac{1}{4}$ pieces instead. It’s either too little or too much.
One powerful tool at our disposal is the rejection method. Let’s keep
rolling the die until we get a number between 1 and 4 included,
rejecting the roll every time it’s a 5 or a 6.
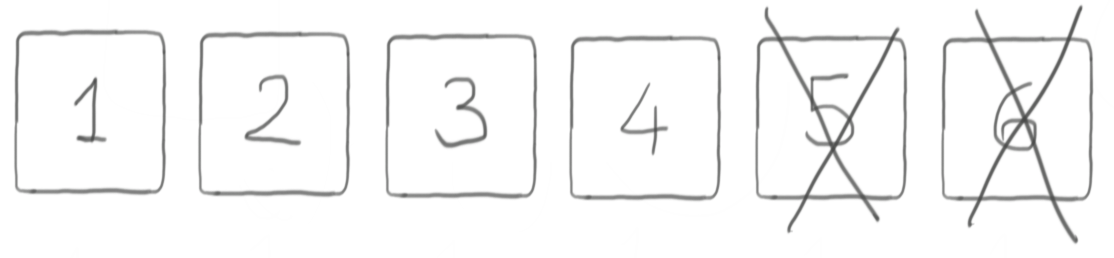
If this gives out anything, it will surely a valid outcome for a D4,
because only admissible values 1 to 4 are allowed. Is it fair
though?
The overall probability of the event value 1 comes out from a roll of
the D6 is still $\frac{1}{6}$, of course. Considering that 1 is also
an admissible value, this is also the same probability as event value
1 comes out of a roll of the D6 AND the outcome of the D6 roll is an
admissible value. The same applies to 2, 3, and 4 of course.
This probability of the union of the two events 1 comes out of the
D6 roll and the D6 roll gives out an admissible value can be
expressed in terms of conditional probability, as in the roll was a
1, subject to the fact that the roll was admissible, which translates
into the following formula:
The conditional probability $P_{1 | {1, 2, 3, 4}}$ is exactly what we are after for establishing the fairness of our virtual D4, because the rejection method ensures us that we got an admissible value (hence, the condition applies). It’s easy to invert the formula, then:
\[P_{1 | \{1, 2, 3, 4\}} = \frac{P_1}{P_{\{1, 2, 3, 4\}}}\]The probability at the numerator is $\frac{1}{6}$. This was easy.
The probability at the denominator is simply the sum of the
probabilities of having a 1, a 2, a 3, or a 4; in the case of a
fair die, it’s $4 \cdot \frac{1}{6} = \frac{4}{6}$.
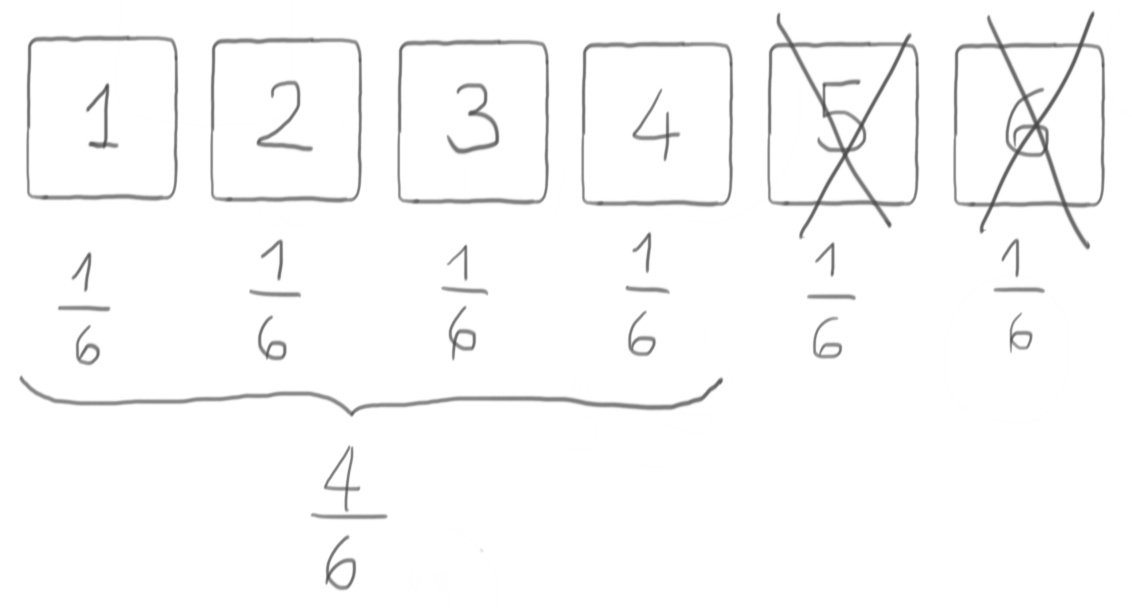
So we end up with this:
\[P_{1 | \{1, 2, 3, 4\}} = \frac{P_1}{P_{\{1, 2, 3, 4\}}} = \frac{\frac{1}{6}}{\frac{4}{6}} = \frac{1}{4}\]The same reasoning can of course be applied to 2, 3, and 4 with
equal conclusions, hence our virtual D4 is, indeed, a fair one
assuming that the starting D6 is fair. Yay!
Conclusions
As we saw, it’s possible to simulate a virtual D4 from a real D6, although there might be some additional rolling involved when we have to reject a specific roll. This happens with non-trivial probability $\frac{1}{3}$ for a single roll, i.e. on average we will have to re-roll one out of three times and still not be sure it will be enough!
Could we end up trapped in a nightmare of rolling over and over without getting anything meaningful for a long time? Sure we could, but the distribution of this is geometric with an average of $1.5$ rolls needed to get something meaninful out, so there should not be too much to worry.
Or should there be?