ETOOBUSY 🚀 minimal blogging for the impatient
Same rejection method?
TL;DR
Where we ask ourselves: did we talk about the same rejection methods lately?
In A 4-faces die from a 6-faces die we introduced a rejection method to generate a D4 die from a D6. Then in Rejection method we took a look at a generalization of that method, to generate samples from an arbitrary (albeit limited in the $x$ axis) probability density.
Are the two really related, though?
The discrete case
First, let’s convince ourselves that the rejection method discussed in Rejection method works equally well for discrete probability densities. As we saw, there are two random draws for each sample:
- one over the $x$ axis
- another one over the $y$ axis.
For discrete densities, instead of using a uniform distribution for the first draw, it suffices to use the equivalent discrete distribution to draw one of the possible discrete alternatives. After that, the procedure on the $y$ axis remains unchanged.
So… D4 from a D6?
Let’s consider a D4 like a D6, where two of the outcomes (namely 5 and
6) have probability to come out equal to $0$.

The enclosing function would in this case be one with value $0.25$ over all six values (in brown below), which corresponds, with proper scaling, to the discrete uniform drawing of our D6:
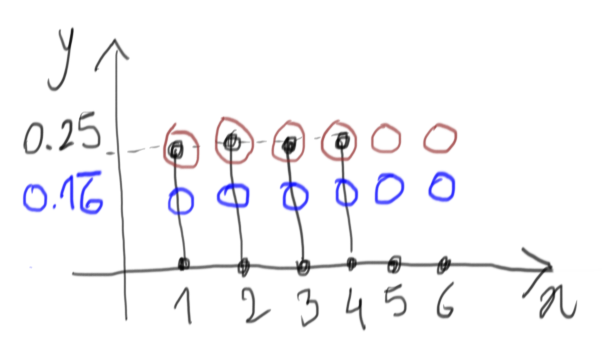
At this point, we can easily see that we don’t really need any random
draw over the $y$ dimension, because it will always lead to acceptance
when the first draw is one of 1, 2, 3, or 4, and it will always
lead to a rejection for 5 and 6. So we can avoid it and fall back
to the method described in A 4-faces die from a 6-faces die. Yay!