ETOOBUSY 🚀 minimal blogging for the impatient
A D4 from a D6, with time guarantees
TL;DR
Generating a D4 from a D6 with the rejection does not give guarantees on time. Can we do something about it?
In previous post a 4-faces die from a 6-faces die we saw a possible procedure to create a virtual D4 from a real D6, by means of the rejection method.
One drawback of this method is that it cannot guarantee us how many rolls will it take to get the next virtual D4 roll. Sure, the probability that it will take more than $n$ rolls is $\frac{1}{3^n}$, which goes down fast, and yet you might have a hard limit on the patience of your players and they might not be happy to know that 1 time out of 27 they will need to roll more than three times that hated D6.
At this point, they might just start thinking you’re so cheap 😡
Let’s take it from another angle
Let’s forget for a moment that we have a D6 and concentrate on our goal. What are we trying to accomplish?
The answer is simple: have a device that is capable of giving us one out of four different symbols, each with probability $\frac{1}{4}$.
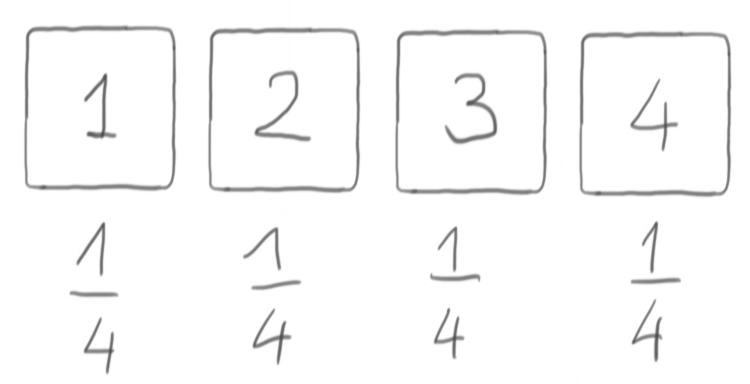
This would be easily accomplished with a coin, for example, because flipping it twice gives us exactly 4 different outcomes, each with our desired probability (assuming the coin is fair):
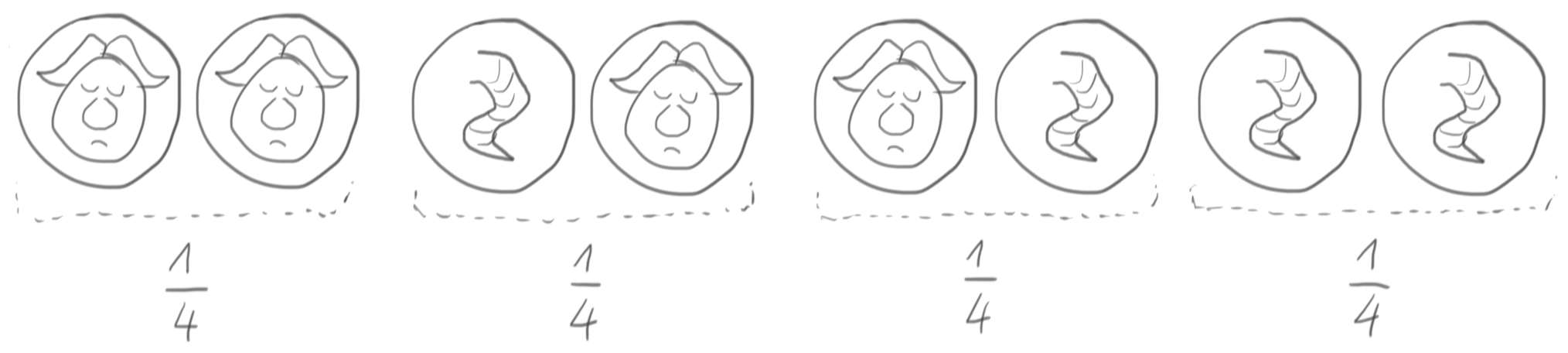
So, let’s use a coin instead…
I guess you know where we’re heading to by now. If you have a coin, you can just use that. But back to our full set of constraints, we don’t have it, we have a D6 instead.
As we saw in the previous post, though, we can indeed use a D6 to generate a virtual coin, and then use this twice to generate a D4.
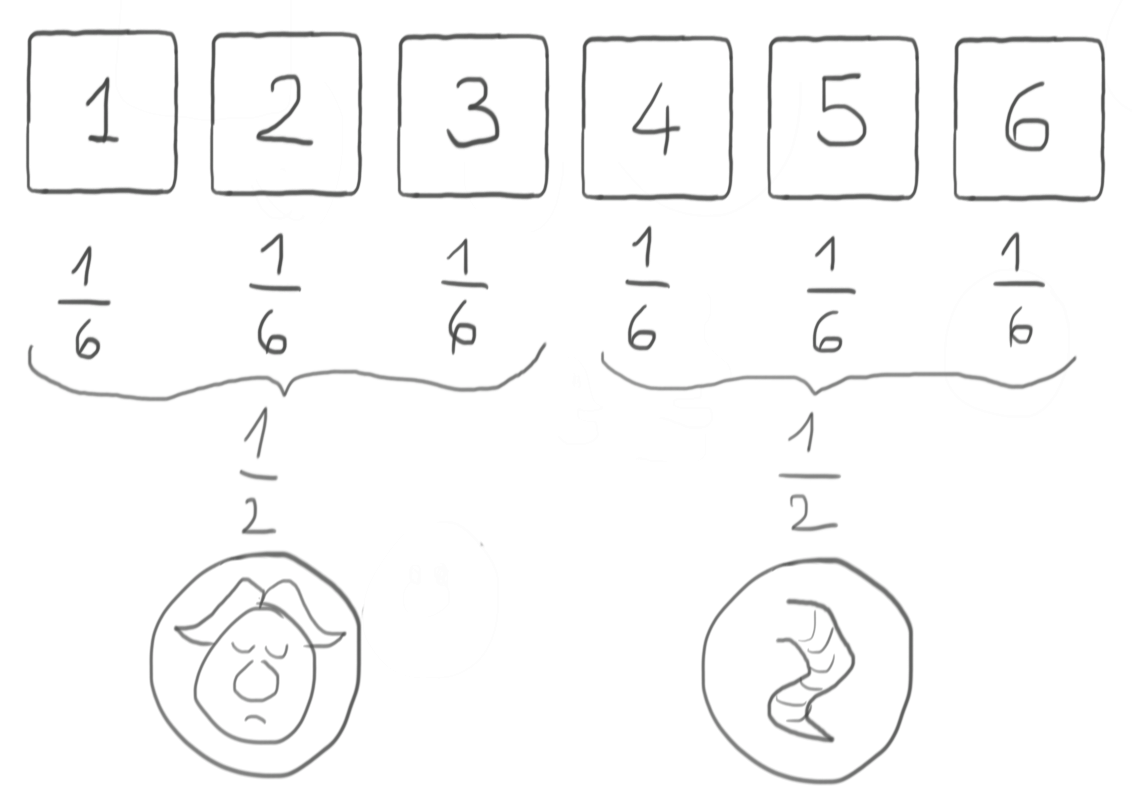
Putting it all together
It’s clear at this point that we can get a D4 by rolling a D6 exactly twice. We can shortcut the virtual coin step and end up with the following algorithm:
- roll a D6 once and note down the outcome as
D6 Roll 1 - roll a D6 once and note down the outcome as
D6 Roll 2 - use the table below to get the result of the D4.
| D6 Roll 1 | D6 Roll 2 | D4 outcome |
|---|---|---|
1, 2, 3 |
1, 2, 3 |
1 |
1, 2, 3 |
4, 5, 6 |
2 |
4, 5, 6 |
1, 2, 3 |
3 |
4, 5, 6 |
4, 5, 6 |
4 |
Can we roll two dice once?
The table in the previous section can prompt us to think: can we roll once using two dice instead? This would save us time and we surely have another D6 somewhere in the house.
The only caveat at this point is that it MUST be possible to tell one die from the other. E.g. you might get them with different sizes, different colors, or mark one of them with a marker. If you can’t do this, you will not be able to distinguish the second and the third case in the table, which will put you in trouble!
What? You don’t have a marker and can’t tell them apart? Well… roll them and use their position with respect to the room to tell which is the first and which is the second - in other terms, get creative!
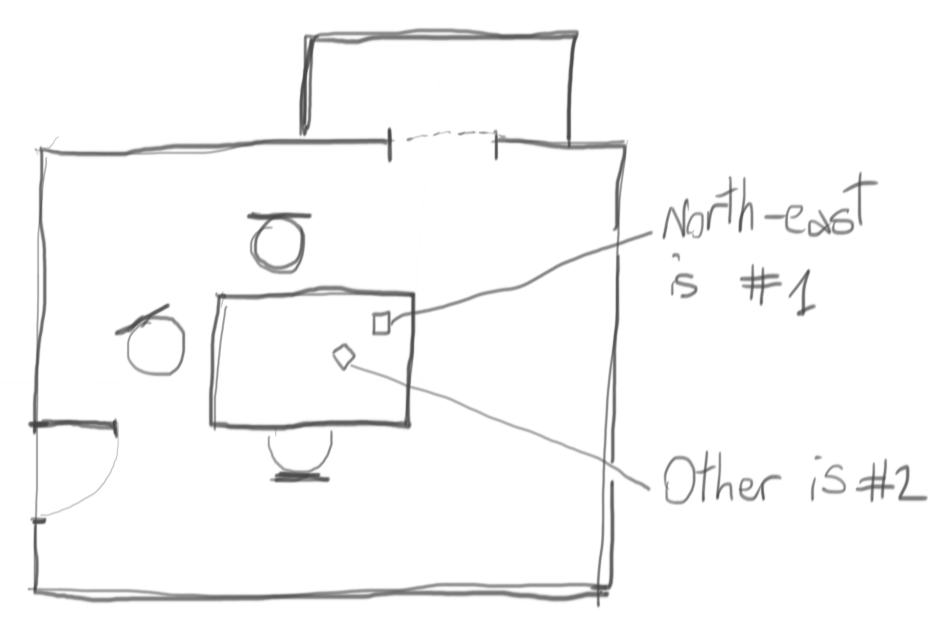
Better than rejection?
From an efficiency perspective, this method is worse than the rejection method, because it always requires two rolls where the rejection method requires an average of $1.5$ rolls instead.
On the other hand, this method has time guarantees, which in some cases might be more important - especially if you indeed have two (distinguishable) dice that you can roll at the same time.
So the answer is actually up to you!